[adsense]
中学受験の勉強をしてくると出てくる「つるかめ算」。
つるかめ算って何だろう、もしくはつるかめ算の解き方で調べている方が多いかなと思います。
この記事ではつるかめ算とはどんな考え方か、解き方も含めて解説しています。
[toc]つるかめ算とは
つるかめ算は小学校の授業では出てこない考え方で、中学受験の問題に登場します。
つるとかめが合わせて18匹います。足の本数が合計50本のとき、つるとかめはそれぞれ何匹でしょう。
このように2つの異なるものの合計が分かっているとき、それぞれの数を出すような問題を「つるかめ算」といいます。
つるかめ算の解き方
つるかめ算は図を使わない方法と、面積図で解く方法があります。上の例文をそれぞれの方法で解いていきます。
方法1、図を使わずに解く
まずすべてかめだったらと仮定して計算します。
全部で18匹で、かめは足が4本なので
18×4=72
全部かめ(かめ18匹、つる0匹)の場合、足の数は72本となります。
問題文の足の合計が50本なので
72-50=22 22本分余計になります。つまりすべてかめではありません。
かめを1匹減らし、つるを1匹増やします。
かめ17匹、つる1匹の場合
17×4+2×1=70
かめ16匹、つる2匹の場合
16×4+2×2=68
・
・
・
合計が50になるところまで繰り返し、答えを求めます。
かめ7匹、つる11匹の場合
7×4+2×11=50
かめ7匹、つる11匹となります。
もっと早く計算するには、
余った脚の本数を、足の本数の差で割ればつるが何匹か計算できます。
つるは2本、かめは4本なので
4-2=2
足の本数の差は2本です。
22÷2=11
つるは11匹、かめは 18-11=7 で7匹となります。
方法2、面積図で解く
上の問題を面積図と表すと、図のようになります。
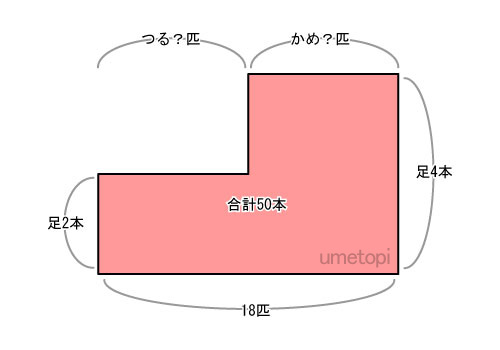
つるとかめの合計を横軸、足の本数を縦軸で表し、合計数を面積に例えて記入しています。
面積は底辺×高さで求められます。
面積は 18×4=72
つまり、すべてかめだった場合は、足の合計が72本になります。
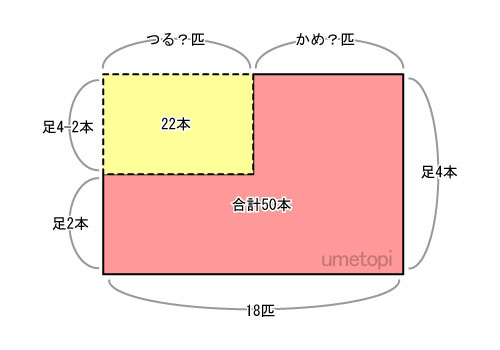
72-50=22
空いている四角の面積(=かめとつるの足の数の差)は22本
面積が分かっているので、横軸(つる?匹)が出せます。
22÷2=11
つまりつるは11匹、かめは18-11=7 で7匹と答えが出ます。
方程式で解いてはいけないの?
知恵袋などを見ると、面積図ではなく方程式に当てはめて解いてはいけないのかという意見がありました。
方程式は中学生になって、はじめてでてくる考え方です。
面積図やつるかめ算は、算数を工夫して解く訓練になります。
方程式では意味の理解していないものでも、覚えさえすれば解けますが、小学生のうちは、なぜそうなるのか、どうして答えを出せるのか工夫して解くことが大切なのではと思います。
大人になってもつるかめ算を使うことがありますが、方程式は覚えていません。それでも、考え方が分かっていれば答えを導きだせます。
つるかめ算を使った実際の難関中学入試問題
つるかめ算がどんな計算方法かわかったところで、実際の難関中学入試問題をみてみます。下記のように出題されていました。
5つの袋ア、イ、ウ、エ、オがあります。それぞれの袋に5gと6gのビー玉どちらかを複数入れました。アから1個、イから2個、ウから4個、エから8個、オから16個のビー玉をとりだし、合計すると176gでした。5gのビー玉はどの袋に入っていましたか。
※一部内容を変えて掲載しております。
上記つるかめ算の解き方と同様、図を使わない方法と、面積図を使った方法で解きます。
図を使わずに解く
まずビー玉の合計数を出します。
1+2+4+8+16=31 で31個。
すべて6gだったらと仮定すると、
6×31=186g
問題文の合計が176gなので、186-176=10
10g多くなりました。だからすべて6gではないことが分かります。
ビー玉の重さの差を求めます。
6-5=1
差は1gです。
先ほど出した重さを差を、ビー玉1個の差で割れば、5gのビー玉の数が出せます。
10÷1=10
5gのビー玉は10個と分かりました。
ア~オの袋には、5gか6gどちらかしか入らないので、合計10になる組み合わせを探します。
2+8=10
つまり、イ、エに5gのビー玉が入っていることが分かりました。
面積図で解く
ビー玉の数は 1+2+4+8+16=31 で31個です。
袋は5つあり、どれがア~オに当てはまるのかは分かりません。図にあてはめると次のようになります。
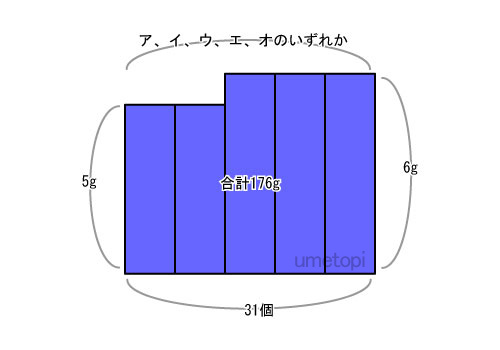
面積を求めます。
31×6=186
つまり空いている部分の面積は
186-176=10
10gだと分かります。
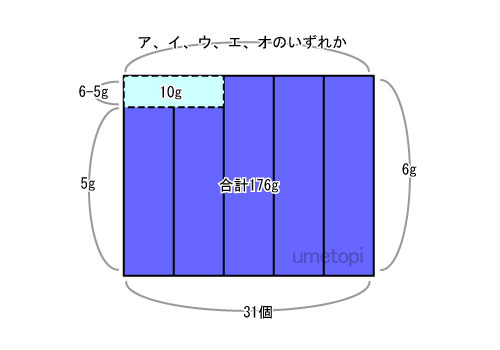
面積10gの縦軸は、
6-5=1 で、1と計算できます。
だから横軸は、
10÷1=10
つまり5gのビー玉は合計10個だとわかります。
ア~オの袋には、5gか6gどちらかしか入らないので、合計10になる組み合わせを探します。
2+8=10
つまり、イ、エに5gのビー玉が入っていることが分かりました。
[adsense]
つるかめ算はややこしい!
つるかめ算で算数につまずき、苦手になる子もいるほど、つるかめ算はややこしい問題です。
でもつるかめ算は日常生活でも使える考え方ですし、中学受験に必要なので、中学受験を考えているお子さんは逃げられない問題です。
そこでおすすめしたいのがZ会です。
Z会の解説が分かりやすかった
難問のつるかめ算ですが、Z会の中学受験コースでは、つるかめ算の仕組みから解説されます。
いきなり面積図で表すのでなく、まずはきちんと考え方を教えるというのがZ会らしい。
一番初めに書いたつるとかめの例文の場合、
まずつる〇匹、かめ〇匹の場合、足の合計は〇本・・・という風に、1つづつ数を減らして答えを求めます。次に、つるとかめを1匹づつ交換するとき、どういった法則が生まれるのか解説します。その法則を利用するためには、どんな式を立てればよいか解説します。
結果、答えが早く導き出せる、という具合です。
解説方法が分かりやすく、基礎から教えてくれるから納得して次に進めるのがZ会の特徴だと、長年続けていて感じます。
→ <どーんとこい!中学入試の算数>第1回 つるかめ算
さぽナビでは、学年ごとに簡単な問題が掲載され、クイズのように楽しめる問題もあります。
例えばこちら→「数のセンスを鍛えよう」
空き時間にお子さんの数のセンスが鍛えられますし、お子さんの算数力で悩んでいる方にはぜひ取り組んでみてほしい問題です。
このようにZ会では考え方の基礎を理解させ、その後つるかめ算であればつるかめ算を使った色んな問題をいくつも解くことで、つるかめ算が身つくようになっています。
つまずきやすい問題も、Z会なら厳選された講師陣が丁寧に解説してくれるから分かりやすいです。
もし市販の教材で勉強を進めているなら、Z会の受講を視野に入れてみてはいかがでしょうか。子ども自身で納得し解決でき、考える力がつきます。
▽Z会については下記記事で詳しく紹介しています。
[st-cmemo fontawesome=”fas fa-arrow-circle-right” iconcolor=”#faa89b” bgcolor=”#eff8fc” color=”#000000″ iconsize=”200″]関連記事:Z会小学生コース。3年以上続けた体験談と入会前にチェックしたい特徴。
関連記事:タブレット学習にはメリットとデメリットがあった!活用法と克服法。Z会小学生コース
関連記事:Z会で中学受験!【入試過去問とZ会の問題】徹底比較[/st-cmemo]